|
In order to assess the occurrence of malaria in West Africa an existing model from the
University of Liverpool is applied. The so-called Liverpool Malaria Model (LMM) simulates the
spread of malaria at a daily resolution using daily mean temperature and 10-day accumulated precipitation
(Hoshen and Morse 2004).
|
|
|
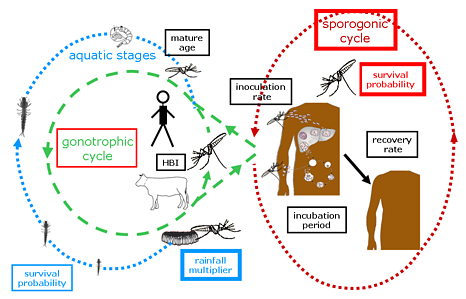
Fig. 1: Illustration of various components of the Liverpool Malaria Model (LMM).
|
The gonotrophic cycle
The model first simulates the egg development within the female mosquitoes, the so called gonotrophic cycle.
The ensuing gonotrophic cycle is temperature dependent and starts at a certain temperature
threshold that is dependent on humidity conditions (Detinova 1962). Since humidity is
often reliant on precipitation a precipitation threshold is defining dry and humid weather
conditions. Using the "degree-day" concept (cp. Glossary) the model is calculating the
daily progress of the egg development within the female mosquito. At the end of the
gonotrophic cycle the mosquitoes oviposit at suitable breeding sites and are
immediately starting a new gonotrophic cycle.
Egg deposition and immature mosquitoes
The egg deposition is dependent on open water bodies that are mostly filled by
precipitation events. At present an accurate simulation of open water bodies as well as the
number of laid eggs is infeasible. These problems were leading to the simplification of the
process of the egg deposition. The oviposition rate is roughly assumed to be proportionate to
both the number of ovipositing mosquitoes and to the decadal rainfall (RRΣ10d).
The model approach implies that no permanent water sources like rivers or lakes are in the
vicinity. Also agricultural activities are neglected, e.g. rice irrigation is affecting the
availability of fresh water and hence the spread of malaria (e.g. De Plaen et al. 2004).
Following the egg stage the mosquito larvae are developing. After a certain time period the
larvae pupate and finally the maturation takes place. The immature mosquito stage is simplified
in the LMM. The process is simply finished after 15 days, and the model assumes a rainfall
dependent per diem survival rate for the immature mosquitoes (s). The probability of survival
varies between about 50% for dry conditions and nearly 100% for periods with abundant rainfall:
s=(RRΣ10d+1)/(RRΣ10d+2).
The sporogonic cycle
The malaria transmission starts in the model when mosquitoes are biting malaria infectious humans.
The course of the infection in the mosquito vector is again modelled via the degree-day concept.
It has long been recognised that the development of sporozoites is temperature dependent
(e.g. Detinova 1962; Snow et al. 1997). The minimum temperature for the development of the malaria
parasite varies experimentally and also among mosquito species (Epstein et al. 1998). There is an
uncertainty about the value of the temperature threshold. Lindsay and Birley (1996) therefore
conclude, that the parasite development ceases below temperatures between 14.5 and 16°C for
Plasmodium vivax and between 16 and 19°C for
Plasmodium falciparum. The setting of the
threshold is important when the malaria is modelled in areas with temperatures in the range of the
minimum temperature (e.g. in the highlands of East Africa). For temperatures well above the
threshold the length of the sporogonic cycle is much less dependent upon the setting of the minimum
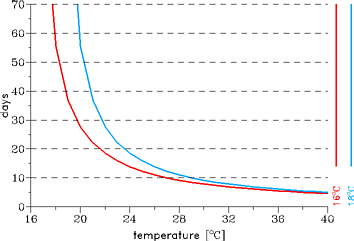
temperature (cp. Fig. 2). Regarding the sporogonic cycle the LMM was originally set by a
temperature threshold of 18°C (Hoshen and Morse 2004). However, modelled temperatures or data
from weather station are unlikely to record conditions in the microhabitats where vectors spend
most of their time (Hay et al. 1996; Kovats et al. 2001). By resting more climatically stable and
warmer houses Anophelines vectors may avoid cold temperatures and thus the restrictions concerning
the progress of the parasite development (e.g. Epstein et al. 1998; Reiter 2001; Koenradt et al.
2006). Therefore the effect of altitude might be partly compensated, when mosquitoes stay in heated
houses (Malakooti et al. 1998). For these reasons the use of 16°C as a temperature threshold
for parasite development is decided. Based on this setting the duration of the sporogonic cycle
lasts about 57 and 13 days at temperatures of 18 and 25°C, respectively (cp. Fig. 2).
|
|
Fig. 2: The effect of temperature on the duration of the sporogonic cycle in days with regard
to different sporogonic temperature thresholds.
|
Mosquito survival
Due to the longevity of the parasite development the mosquito survival probability is of great importance.
The age structure of Anopheline females and survival rate exerts a strong influence on the reproduction
rate of the mosquito population and the spread of the malaria parasite. Hence the vector survivorship is
of paramount ecological importance for the distribution of malaria (e.g. Service 1976; Clements und
Paterson 1981; Lee et al. 2001; McKenzie et al. 2002; Scholte et al. 2003). The survival depends on
characteristics of the mosquito species, the activities of individuals, climate, the incidence of
parasites, and predators (Boyd 1949) and the age of the mosquito (e.g. Samarawickrema 1967). Most of these
factors are elusive and are only indirectly taken into account in malaria models. The LMM is only
considering the weather impact on vector survivorship.
However, the relationship between mosquito survival and humidity is unclear (Lindsay
and Birley 1996), and therefore the humidity is not taken into account in the numerical LMM setting.
Various mosquito survival probability schemes have been developed with regard to the modelling of malaria.
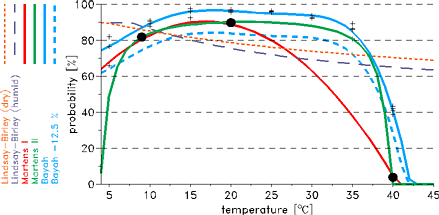
In the LMM five different schemes are implemented, these are: the so called Lindsay-Birley, the Martens I,
the Martens II, the Bayoh, and the Bayoh-12.5% scheme (Fig. 3). Initially, the LMM was set by the
Lindsay-Birley scheme (Hoshen and Morse 2004 and 2005), that assumes a constant mosquito survival of 50% per
gonotrophic cycle. However, the application of this scheme is not possible at very high temperatures.
Due to the scarce information regarding the temperature dependence of the mosquito survival the literature
(e.g. Craig et al. 1999; Hay et al. 2000a) refers to studies published by Martens
(Martens et al. 1995a and 1995b; Martens 1997). Martens (1997) states: "Relying on data reported by
Boyd (1949), Horsfall (1949), and Clements & Patterson (1981), we assume a daily survival probability of
0.82, 0.90 and 0.04 at temperatures of 9°, 20° and 40°C, respectively, expressed as:
p=exp(-1/(-4.4+1.31 T-0.03 T2.
The Martens I scheme was obviously generated as a polygon connecting the quoted three data points in
the T-pd-diagram (Fig. 3). The formula provided by Martens (1997)
was not considered and is leading to different survivorships, the so called Martens II scheme.
The main difference between the Martens I and Martens II scheme is the more smoothly decrease of the
survival probabilities for higher temperatures.
Bayoh (2004) observed the survival and mortality rates of
Anopheles gambiae sensu stricto in environmental
chambers at combinations of temperatures from 0 to 45°C at 5°C intervals and relative humidity's
of 40%, 60%, 80%, and 100%. Using the data of these experiments and assuming an exponential model of
mortality it is possible to derive daily vector survival probabilities. The values are used to define a
polygon regarding Anopheles gambiae sensu stricto
survivorship in the laboratory, the so called Bayoh
scheme (Fig. 3). However, vector survival is higher in captivity than in the wild (e.g.
Clements and Paterson 1981) and hence has to be reduced.
The shift-off is arbitrarily set to 12.5%. The probabilities of the Bayoh-12.5% scheme compare well
with field observations. The Bayoh-12.5% scheme agrees also fairly well with the mean daily survival of
84.6% found by Kiszewski et al. (2004).
As shown here, all the presented schemes regarding mosquito survival are not fully satisfying. Therefore
the incorporation of upcoming new information is essential in future refinements of the LMM.
|
|
Fig. 3: Illustration of different schemes regarding the daily mosquito survival (in %) against
the daily mean temperature (in °C). Displayed is also the data basis of the two Martens schemes
(the three black dots).
|
Malaria infection of humans
After the completion of the sporogonic cycle the mosquitoes are able to transmit the parasite to a human.
When an infected female mosquito is biting one of the 100 humans of the model the parasite is transmitted
with a certain probability. The so called inoculation rate is set in the LMM by the default value of 50 %.
All the infected human hosts are entering the latent phase. The parasite development within the human host
lasts about two weeks (Hoshen and Morse 2004). In the model infected humans are infectious at day 15 and
are at that time able to infect mosquitoes with the male and female gametocytes until these sexual forms of the
parasite vanish. Humans becoming infectious increase the so-called malaria prevalence, i.e. the proportion
of the 100 humans that are carrying gametocytes. Malaria clearance is a slow process sometimes continuing
several months or even years (Sama et al. 2004). In the model the daily infection survival rate (d) is
0.9716 and is consistent with malariotherapy (Hoshen and Morse 2005). The exponential decay reflects a
probability of about 90% of an individual clearing an untreated infection within 80 days.
In areas of high infection pressure the prevalence is often constant for a certain time. The
equilibrium condition is reached, when all the modelled humans are either infected or infectious.
During that time the numerous infectious mosquitoes are again infecting every human clearing the parasite
prevalence. Due to the fixed recovery rate only 64.9% pass the latent period and will become infectious.
That is the reason that for saturated conditions the malaria prevalence is not getting higher than 64.9%.
Summing up, the LMM is simulating the malaria transmission within the human and mosquito population and
is only forced by two meteorological variables, daily mean temperature as well as daily precipitation
amounts.
Sensitivity of the LMM
Various sensitivity experiments reveal that LMM is fairly sensitive to the setting of some of the
model parameters. The proportion of the population that is carrier of the
malaria parasite strongly depends on the applied mosquito survival scheme. In addition the malaria
transmission as simulated by LMM strongly depends on the recover rate (r=0.0284) of humans.
Furthermore, in areas where temperature is not a factor the simulated malaria transmission from
mosquitoes to humans is mainly governed by the model rainfall multiplier that couples the
precipitation with the oviposition of female mosquitoes and ultimately determines the size of
the mosquito population. At high altitudes, the sporogonic temperature threshold, i.e. the
minimum temperature for malaria parasite development in the mosquito, is of importance. Unlike in
the model version described by Hoshen and Morse (2004) the LMM was parameterised by a different
mosquito survival scheme and a sporogonic temperature threshold of 16°C.
Original and interim LMM settings
|
